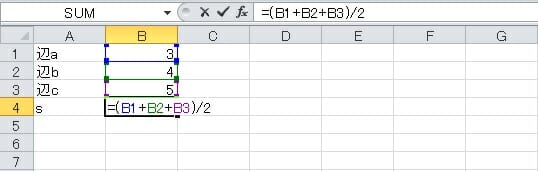
角度、辺と三角形の面積を計算します CalcProfi オンライン計算機 言語: 私の電卓 お気に入りに追加 お気に入りから削除 三角形の計算 三角形の計算は、計算して見つける:角、辺、三角形のすべてのタイプのエリア。計算:直角三角形、両面三角形、二等辺三角形や正三角形を。 3つの不等辺三角形の選択した3つの入力値から他の要素の値を計算します。 直角三角形の計算機 底辺・高さ・面積・角度を計算 かんたん計算機 目次 底辺と高さから面積と角度と斜辺の長さを求める 三角形の3つの辺がa = 3、b = 4、およびc = 5であるという問題が発生したとします4 角度 (θ) =DEGREES (ATAN ( B2/B1 )) 5 面積 (S) =1/2 * B1 * B2 不等辺三角形 ヘロンの公式 (三角形の3辺から面積・角度・高さ) 面積
斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める
不等辺三角形 辺の長さ 計算
不等辺三角形 辺の長さ 計算-「三角形の辺 と 1辺2角を使って他の辺の長さを求めるときには、 正弦 sin60°なら計算できるけれど、sin75°の値は勉強していないよ。というわけでここは、 と に注目して、正弦定理を使おう。 これでaも求められた。あとはbだけだ。でも、この bはちょっと厄介sin75°もcos75°も値はわから正弦定理で辺の長さを求めるときに,立式はできるのですが, 正弦定理 を b =〜 の式に変形できません。 答えを見ても,変形途中の過程がよくわからないので詳しく教えてください。 というご質




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比
<不等辺三角形> 3辺(ヘロンの公式)、2辺と高さ、2辺と夾角、辺と高さと角、2角と夾辺、2角と高さ、それぞれから各種計算 計算結果:辺、高さ、各角度、面積、周囲の長さ <四角形・多角形> ・正方形、長方形、ひし形、平行四辺形(2辺と夾角)、正多角形、それぞれから各種計算 計算結果:面積、周囲の長さ ・台形、平行四辺形(底辺と高さ)、それぞれすなわち、三角形を構成する3辺の長さを a,b,c とするとき、次の三つの不等式が成り立つ。 a < bc; 赤い線で示すように、三角形と平行四辺形に分けます。 三角形の三辺の長さは26、65、67となります。 ここでヘロンの公式を使って三角形の面積を出します。 S=√(s・(sa)・(sb)・(sc)) Sは求める面積、a、b、cは辺の長さです。sは下式です。 s=(1/2)×(abc)
「辺(へん)」の長さが揃ったものの名前をよく見る気がします。 ですが当然、このように揃った三角形ばかりではありません。 「どの辺もそろってない」という三角形も存在します。 その名も「不等辺三角形(ふとうへんさんかっけい)」。 字の通り、どの辺も等しくない三角形ですねで計算できちゃうんだ。 ガンガン問題をといていこう! そんじゃねー Ken 頂角の求め方、二等辺三角形との関係 頂角の求め方を下式に示します。 頂角=180°-2×底角 三角形の内角3 おかしな不等辺三角形 パラドックス 「不等辺三角形が二等辺三角形になる? 」 二等分線との交点をD とします。 図1は点D が三角形の内部にある場合、図2 は点D が三角形の外部にあ る場合を示しています。 となります。 となります。
大半の書物や 三角形のどの辺の長さも他の二辺の長さの和より小さい。すなわち、三角形を構成する3辺の長さを a,b,c とするとき、次の三つの不等式が成り立つ。 a bc b ac c ab この関係は三角不等式として一般化される。 三角形の2辺の和と差 三角形の3辺の長さについて以下の定理が成り立つ。 三角形の2辺の長さの和は、他の1辺の長さより大きい。 三角形の2辺BH=xとおいて (このときCH=6xとなります) AHの長さ (の2乗)を2とおりの方法で表わせば解けます。 (√13) 2 x 2 = AH 2 = 5 2 (6x) 2 (√13)2x2 = 52 (6x)2 13x 2 =25 (3612xx 2 ) 24=12x x=2 (√13) 2 2 2 =AH 2 AH=3浅見光彦シリーズ「不等辺三角形」が楊輝荘などで撮影されました。 楊輝荘を「陽奇荘」として、物語の柱として登場してまいります。 楊輝荘の聴松閣・白雲橋や、松重閘門など歴史的建造物が撮影場所になり、 そのほかにも日泰寺や中川警察署など登場してまいります。 《番組名》 フジ
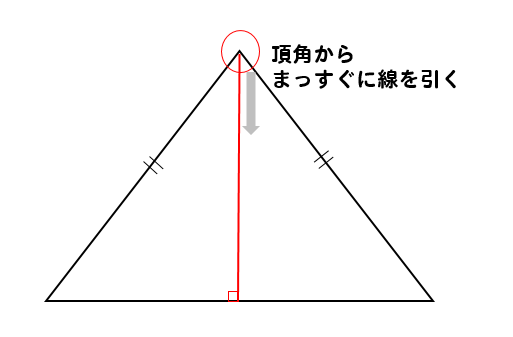



高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ




種明かし Imujii S Page
三角形の3つの辺がa = 3、b = 4、およびc = 5であるという問題が発生したとします。 三角形の半周長を計算します。 三角形の半周長を見つけるための方程式は次のとおりです。 S = a b c / 2。まず、三角形の3辺すべてを合計します。これは、a b cを意味します。 3つの数値をすべて合計したら、合計を2で割ります。例を見てみましょう。 不等式を三角形の各辺の長さ a, b, c a, b, c a, b, c のみで表してから3変数の不等式を代数的に証明する, というのが幾何不等式証明のもっとも基本的なパターンです。 三角形の面積を三辺の長さで表すといえばヘロンの公式が思いつきます。 三角形の公式が使える条件 c^2=a^2b^2 上記で、三角形の各辺の長さがわかる条件を教えてください。 ちょっと見た感じですと、どこか一つの内角が90度であればいいような気がするのですがどうでしょうか?



二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




直角三角形 辺の求め方 直角三角形 辺の求め方 直角三角形 高さがx 底 Okwave
まとめ:直角二等辺三角形の辺の長さの求め方は2通りでクリア! 直角二等辺三角形の辺の公式はシンプル。 斜辺を求めるとき → √2をかける;概要 三角形の三辺が x, y, z で最大辺が z とすれば、三角不等式は z ≤ x y {\displaystyle z\leq xy} が成り立つことを主張している 。 等号 が成立するのは三角形が面積 0 に退化したときに限る。 ユークリッド幾何学 ほかいくつかの幾何学において、三角不等式は距離に関する定理であって、ベクトルやベクトルの長さ( ノルム )を用いて ‖ x y ‖ ≤ ‖ x ‖ ‖ y正弦定理から,三角形の辺の長さを求める計算について ABCにおいて a = 3 , A = 60°, B = 45°のとき b を求めよ。 という問題がありますが, これを定理にあてはめていって, b = 3 / sin60°× sin45° まではつくれるんですが,そこから (3 ÷ √3/2 ) × 1/√2= 6/√6=√6 というのになるのが,意味がわか




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく
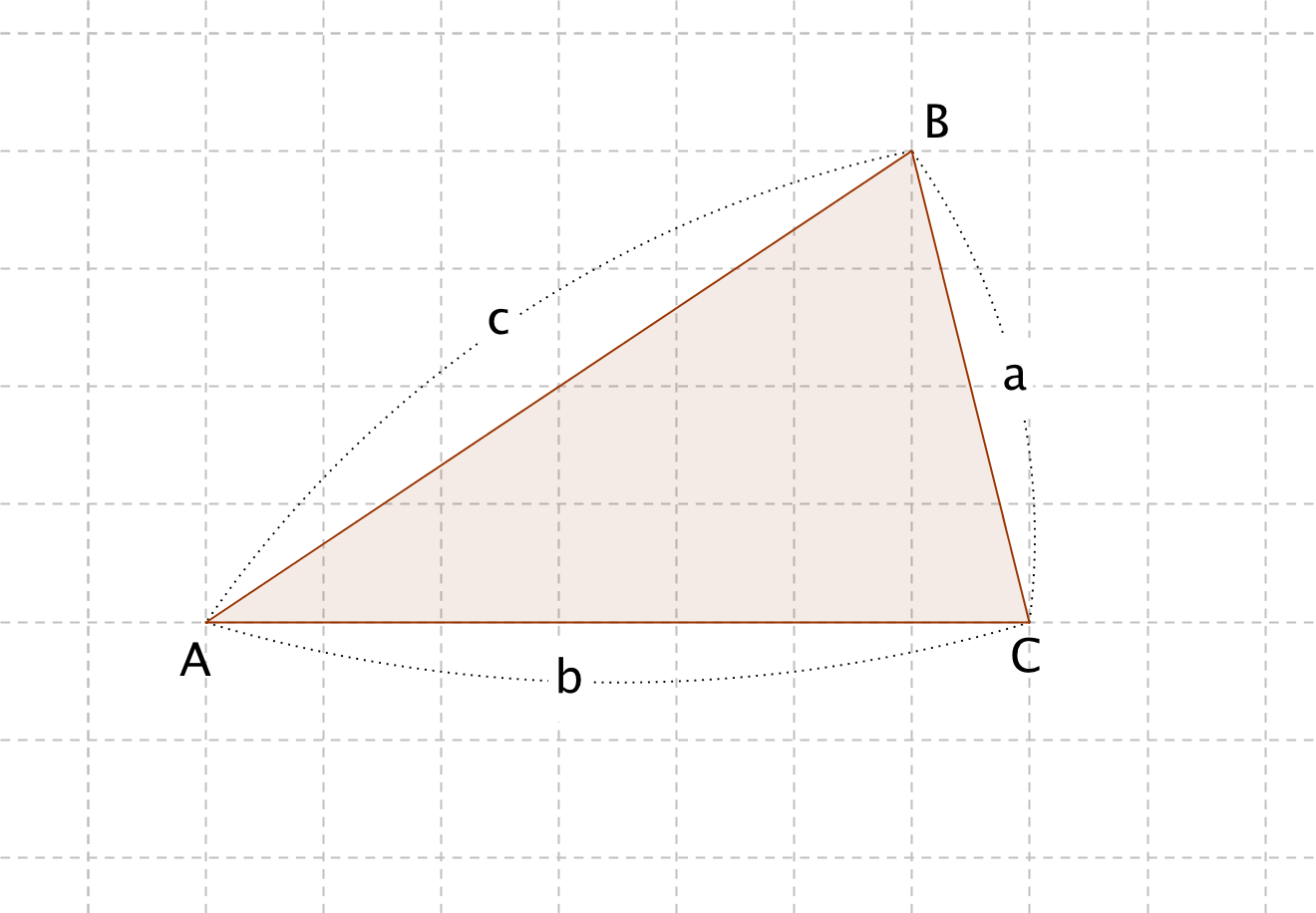



C言語入門 入力した3辺の長さから三角形の種類を判別 Webkaru
正方形の面積 A: 面積: 長方形の面積 A: B: 面積: 円 円 半円 扇形 円周長から面積 四角形 四角形 四角形 4辺と対角線 角パイプ 三角形 三角形 三角形(3辺) 四角形 平行四辺形四角形 4角形 面積計算 公式 求め方 正方形 長方形 縦 横 自動 area 面積 四角形 面積; こんにちわ。 正弦定理と余弦定理を使えばいいのですが、コツがありますね。 ・向かい合う角と辺について、角の大きさと辺の長さがわかっているときには正弦定理を ・2辺の長さとそのはさむ角の大きさがわかっているときには余弦定理をあてはめればいいと思います。 たとえば、質問で書かれていた場合であれば、 >普通の三角形の一辺と2角が分かる場合



不等辺三角形の面積の計算の仕方をおしえてください 不等辺三角形の Yahoo 知恵袋
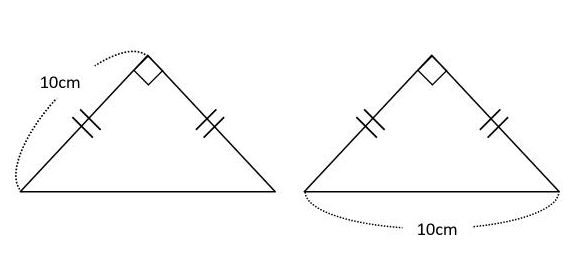



二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
4 9 = c × c 13 = c × c よって、長い辺の長さは c = 13 (二乗して 13 になる正の数)となります。 では、 13 はどれくらいの長さでしょうか? 3 × 3 = 9 c × c = 13 4 × 4 = 16 なので、 13 は 3 より大きくて 4 より小さい数だと分かります。 もう少しきちんと計算すると、具体例で学ぶ数学 > 図形 > 直角二等辺三角形の辺の長さの求め方 最終更新日 直角二等辺三角形において、 (斜辺の長さ) = 2 × (他の辺の長さ) ( 2 はだいたい 14 ) 目次正三角形の面積から1辺の長さと高さを計算します。 正三角形の面積を入力し「正三角形を計算」ボタンをクリックすると、入力された面積から1辺の長さ、高さを計算し表示します。 面積 S: 面積Sが1の正三角形 1辺の長さ a: 高さ h:




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット
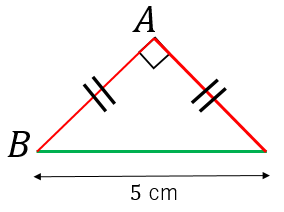



直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学
それでは,三平方の定理を利用して,実際に直角三角形の辺の長さを求める練習をしてみましょう。 右の図のように,∠C =90 °の直角三角形ABC の辺BC 上に 点D がある。AB 5 5= cm,BD=6cm,DC=4cmのとき, AD の長さを求めなさい。 a b c BC a a a a b b b b c 1 三平方の定理 BCD A 6cm 4cm 5 5 cm *「要点」は三角形の3つの辺の長さを測れば、面積はかんたんな計算で出せます。そうやって、すべて 三角形の外周を求めるとは、3辺の長さの合計を求めるということです。1 3辺全ての長さを単純に足していくというのが基本ですが、自分で辺の長さを求めなければならない事もあります。 この記事では三角形の2辺の和と差 物理学のフィロ 直角三角形の高さは?1分でわかる計算、求め方、公式




Triangle Select En App Store




黄金三角形による18 シリーズの三角比 おいしい数学
余弦定理を変形すれば、 b , c , a が分かっているときに A を求めるという使い方もできます: a 2 =b 2 c 2 −2bc cos A この式をよく見ると、 「右辺は辺の長さだけ」 でできており、 左辺は角度だけ でできています。 したがって、この式を利用すると 「3辺の長さ」から、 「角 A 」 を求める ことができます。 (正確には、角 A そのものではなく cos A が求まりますが 対角線の長さ=√2×(1辺の長さ) となります。 よって下図のような正方形においては、対角線BDの長さXは、√2aです。 なぜこのような公式が導かれるかといえば、対角線と正方形の2辺で作られる直角三角形で三平方の定理を使っているだけです。不等辺三角形 著者名 著:内田 康夫 発売日 12年04月06日 価格 定価:1,122円(本体1,0円) isbn 9754 判型 新書 ページ数 296ページ シリーズ 講談社ノベルス 初出 10年4月に小社より単行本として刊行されたものを、ノベルス化したもの。
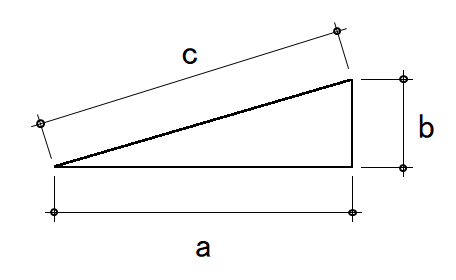



建築積算の数量算出中によく使う計算 直角三角形の斜辺の長さ




三角形の面積は 正三角形 二等辺三角形の面積式の計算は
・正三角形(面積から辺と高さ) 正三角形の面積から1辺の長さと高さを計算します。 直角三角形 ・直角三角形(底辺と高さ) 直角三角形の底辺と高さから、斜辺と角度と面積を計算します。 ・直角三角形(底辺と斜辺) 直角三角形の底辺と斜辺から、高さと角度<不等辺三角形> 3辺(ヘロンの公式)、2辺と高さ、2辺と夾角、辺と高さと角、2角と夾辺、2角と高さ、それぞれから各種計算 計算結果:辺、高さ、各角度、面積、周囲の長さ <四角形・多角形> 正方形、長方形、ひし形、平行四辺形(2辺と夾角)、正多角形、それぞれから各種計算 計算結果:面積、周囲の長さ 台形、平行四辺形(底辺と高さ)、それぞれから不等辺三角形 高精度計算サイト 角度の計算と斜辺、高さの関係は?3分でわかる計算(求め方 エクセルで2辺の長さがわかってる直角三角形の角度を求めるに 直角三角形の計算機 底辺・高さ・面積・角度を計算 かんたん 三角形の計算|計算サイト ;
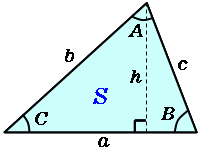



不等辺三角形 高精度計算サイト




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比
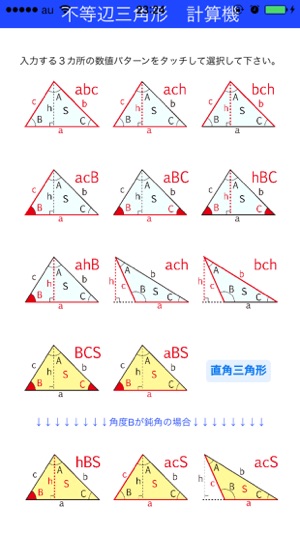
不等辺三角形の選択した3つの入力値から他の要素の値を計算します。 入力指定 3辺abc 2辺abと高さ (Cは鋭角) 2辺abと高さ (Cは鈍角) 2辺bcと高さ (BとCが鋭角) 2辺bcと高さ (BかCが鈍角) 2辺abと夾角C 辺aと高さと角C 2角BCと夾辺a 2角BCと高さ 面積と2辺ab (Cは鋭角) 面積と2辺ab (Cは鈍角) 面積と2角BC 面積と辺aと角C 面積と高さと角C三角形がによって形成されていると仮定します 側 62センチ、片側42センチ、片側51センチ。 3辺の長さが異なるため、不等辺三角形になります。 同様に、角度について表現されていることによれば、三角形の内角が67度、42度、110度の場合、不等辺三角形としても分類されます。




小5 算数 小5 42 三角形の面積 Youtube



1
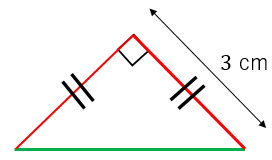



直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学




二等辺三角形の面積を求める算数の公式は



11 7 数学 図形 これは 不等辺三角形 ふとうへんさんかっけい ですか 辺が揃ってない三角形の話 のっぽさんの勉強メモ



斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



このように 不等辺三角形の2つの辺の長さと その間の角の Yahoo 知恵袋




小学6年生で三角形の面積求め方わかりません 小学6年生の親です 学 数学 教えて Goo




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比
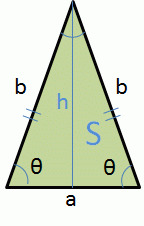



三角形の公式 Wakatta
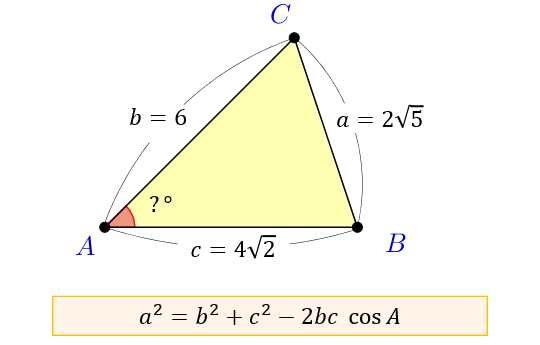



余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
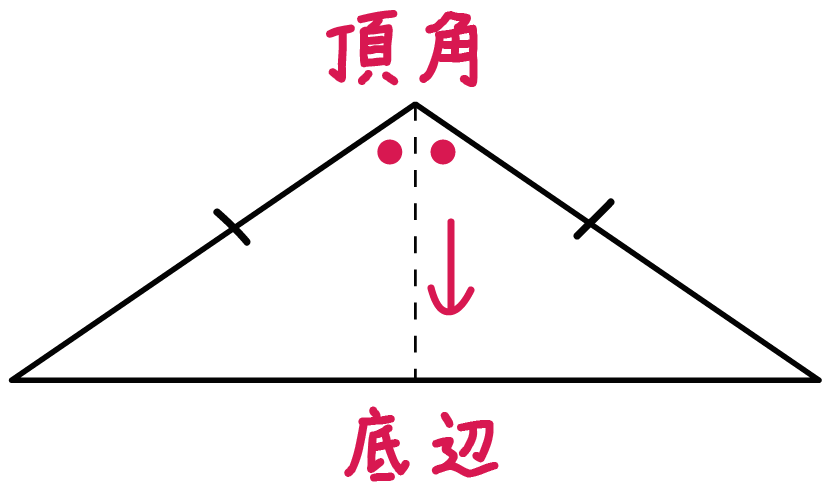



二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




直角三角形 Wikipedia
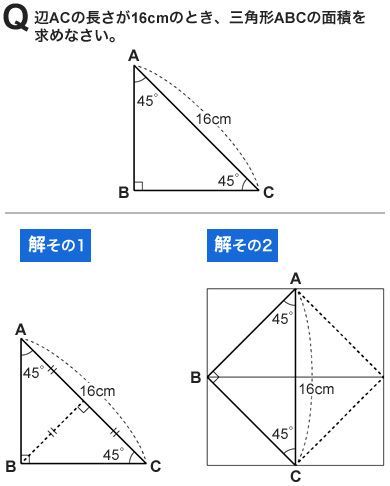



ベストコレクション 不等辺三角形 高さ 求め方 不等辺三角形 高さ 求め方 小学生
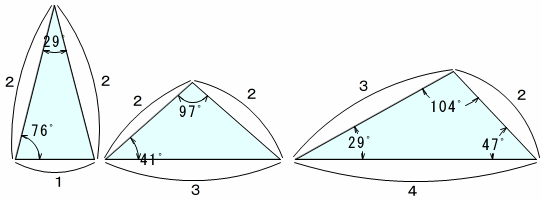



3 4 5の三角形で 本当に直角ができる Note Board



Q Tbn And9gcq7h6dlzvq5e0plulfvxu64dpvadasyky0sizoi2drjv Uyz1m5 Usqp Cau
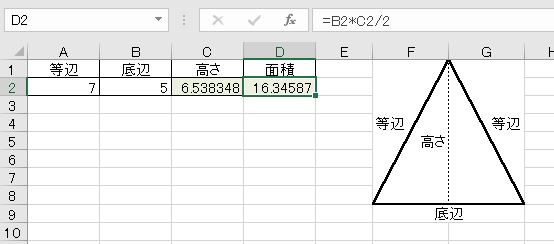



Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
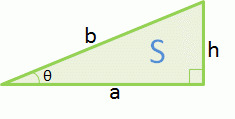



三角形の公式 Wakatta




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比
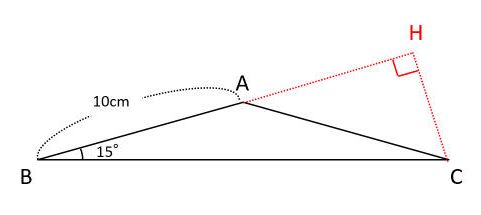



二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ



斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める




直角三角形の辺を求める Youtube




簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく
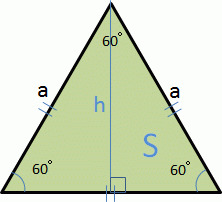



三角形の公式 Wakatta
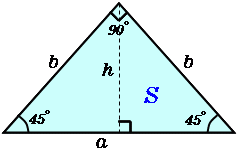



三角形 高精度計算サイト




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ



三角形の計算 Google Play のアプリ



二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係
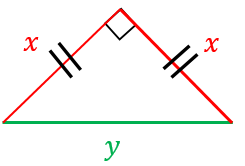



直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学




辺の長さが全て整数となる直角三角形と二等辺三角形で周の長さも面積も共に等しい組 あなたも社楽人
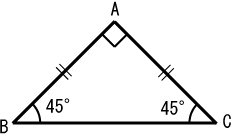



直角二等辺三角形 Wikipedia



斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める




簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく



三角形 辺 の 長 さ 比率 238n424 Proxydns Com
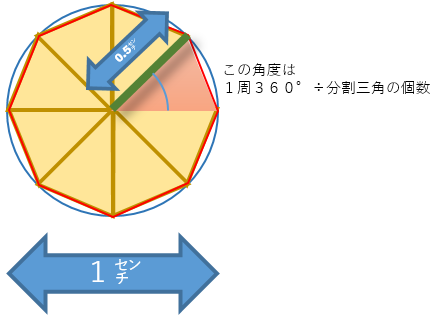



円周率を疑ってみた Officeの魔法使い



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
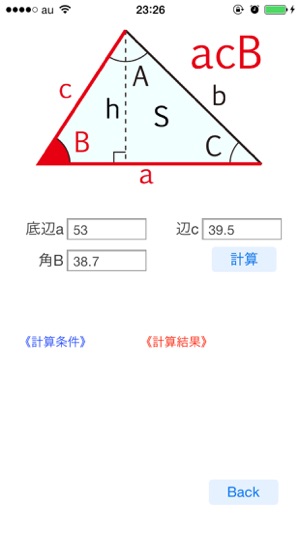



Triangle Select En App Store
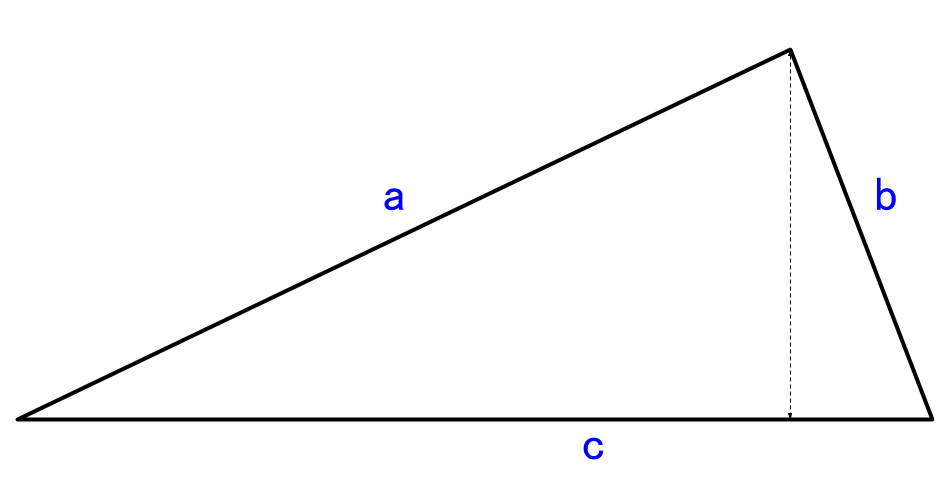



ヘロンの公式 計算機 三角形の面積と高さを 3辺の長さから計算します やまでら くみこ のレシピ
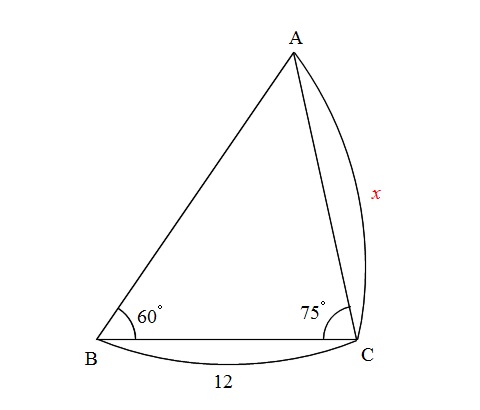



三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない




直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学




数学 中3 61 三平方の定理 基本編 Youtube




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ
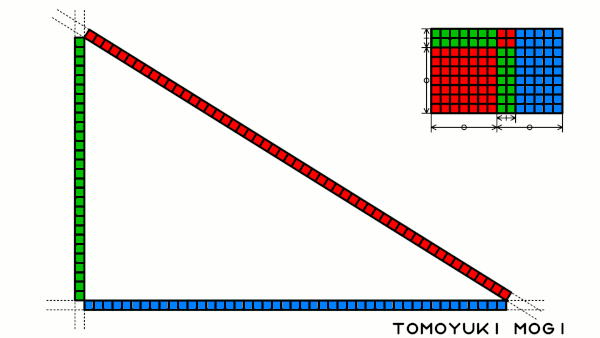



直角三角形 Wikiwand




不等辺三角形 至急ご回答お待ちしております 不等辺三角形について その他 学校 勉強 教えて Goo




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




建築積算の数量算出中によく使う計算 直角三角形の斜辺の長さ
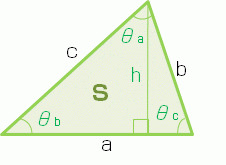



三角形の公式 Wakatta




中学数学 直角三角形の辺の長さの求め方 超丁寧に なぜか分かる はかせちゃんの怪しい研究室



ヘロンの公式 不等辺三角形などの面積 角度 高さ 数学 エクセルマニア
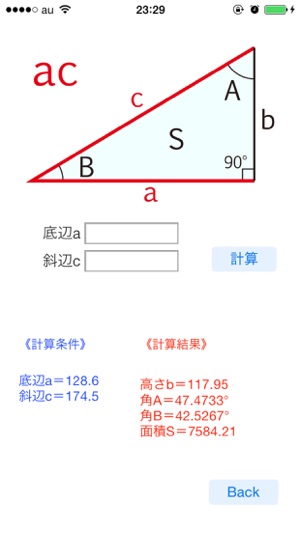



Triangle Select En App Store




不等辺三角形の欠けている辺の長さ 21
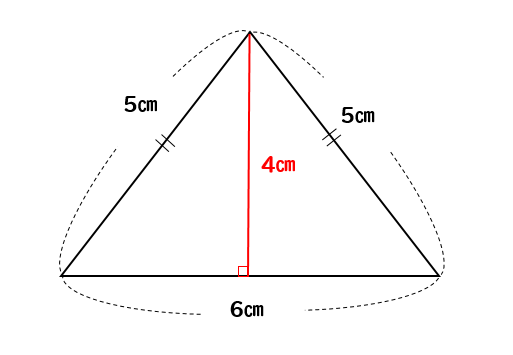



高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



不等辺三角形の高さについてです 画像のa B C 角a Yahoo 知恵袋
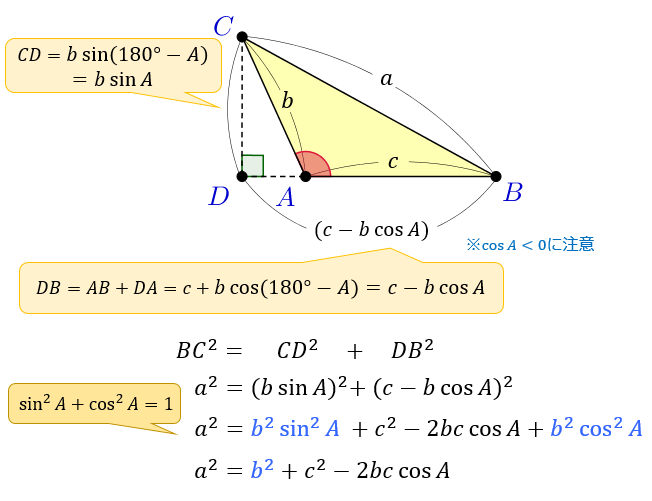



余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ




高校1年生数学の問題です 1 直角を挟む2辺の長さの和が16である直角 中学校受験 教えて Goo




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集
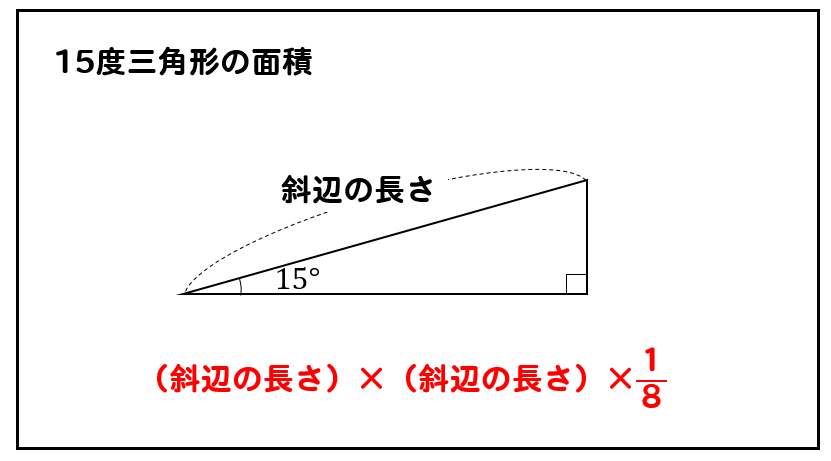



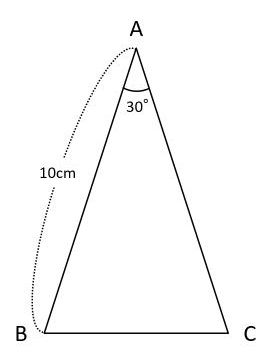
小学算数 15度 75度の三角形ってどうやって面積求める 数スタ



3



よろしくお願いします 画像の通り 二等辺三角形の底辺の長さの求め方 計算 Yahoo 知恵袋
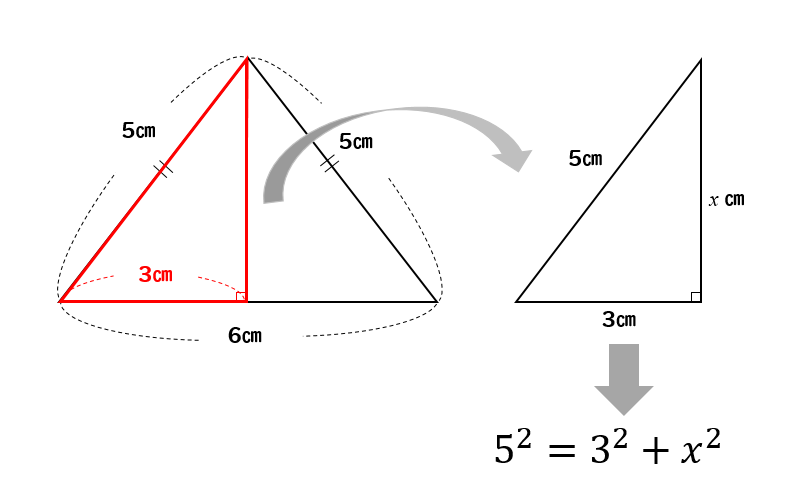



高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ
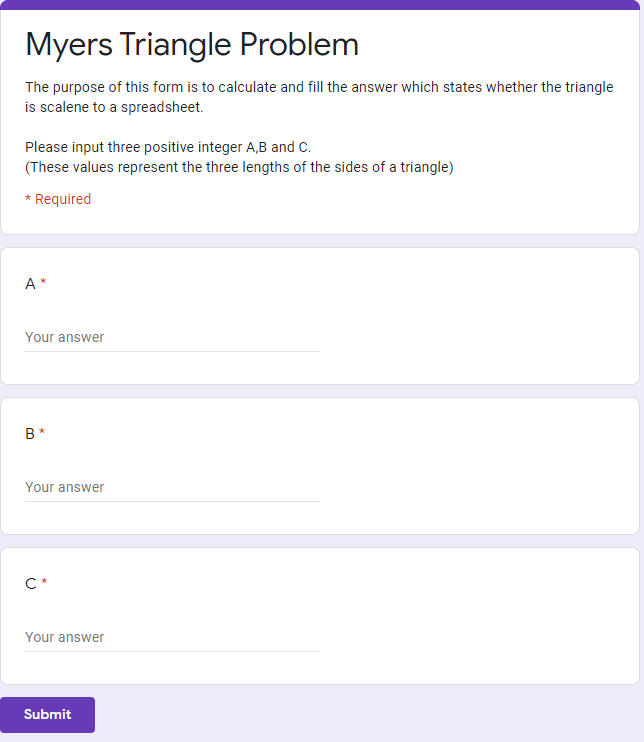



マイヤーズの三角形の問題のテスト対象を Google Formsで作る




黄金三角形による18 シリーズの三角比 おいしい数学
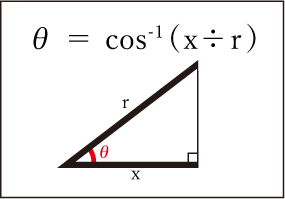



三角関数をマスターしよう その3 金属加工 ものづくり初心者のメモ帳 Mc マシニングセンター Ncプログラムの学習




三角形の面積は 正三角形 二等辺三角形の面積式の計算は




三角比 30 45 60 もう一度やり直しの算数 数学




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



Triangle Select En App Store




3 おかしな不等辺三角形 Imujii S Page




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく



1
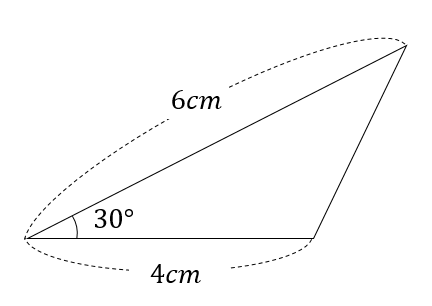



小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ




最高 50 正三角形 面積 求め方




頂角36度の二等辺三角形の辺の比を教えてください 頂角36度の二等辺三 数学 教えて Goo
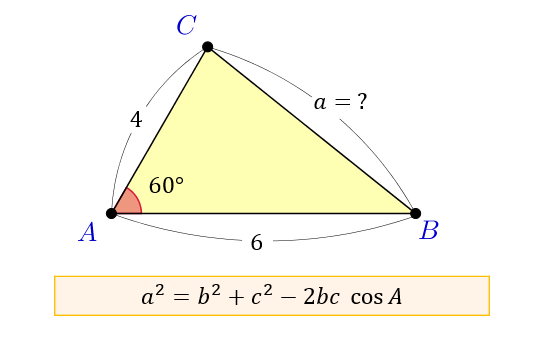



余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ



ヘロンの公式 計算機 三角形の面積と高さを 3辺の長さから計算します やまでら くみこ のレシピ



二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係




二等辺三角形 Wikipedia



Www Yama Kyoukai Jp Download File Id 1923



このように 不等辺三角形の2つの辺の長さと その間の角の Yahoo 知恵袋




余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ




基本のtriangles 三角形 に関する英語表現をマスターしよう ゆう アメリカ生活終了 英語勉強



0 件のコメント:
コメントを投稿